三角形の面積比を求める基本的な考えを3つ紹介します。入学試験にも三角形の面積を求める問題は数多く出題されています。
その面積を求める際に単純に公式通りに底辺と高さを用いる方法もありますが、ベースとなる三角形の面積の何倍になっているのか、面積比を求めることで簡単に解答に辿り着くこともあるので是非覚えていただきたい。
高さが同じ三角形の面積比
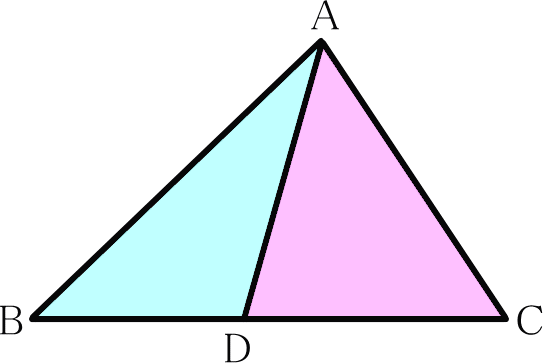
三角形の面積は「底辺×高さ÷2」で求めることができます。
この図の△ABDと△ADCは高さが同じなので底辺の比がそのまま面積の比になります。
△ABD:△ADC = BD:DC
また、△ABCと△ABDの面積比も底辺の比がズバリ面積の比になるので面積比は次のようになります。
△ABC:△ABD = BC:BD
一辺を共有する三角形の面積比
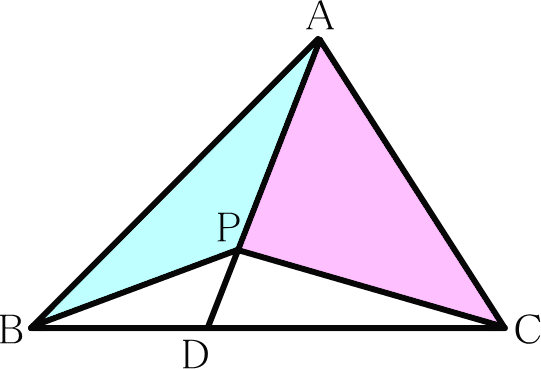
こちらは辺APが2つの三角形の共通となっています。
前述した通りまず△ABD:△ADC = BD:DC です。また不要な部分の三角形 △PBDと△PCDの面積比も同様の考えで△PBD:△PDC = BD:DCです。
全体の面積比も不要な部分の面積比もBD:DCです。
したがって △ABP:△APC = BD:DC
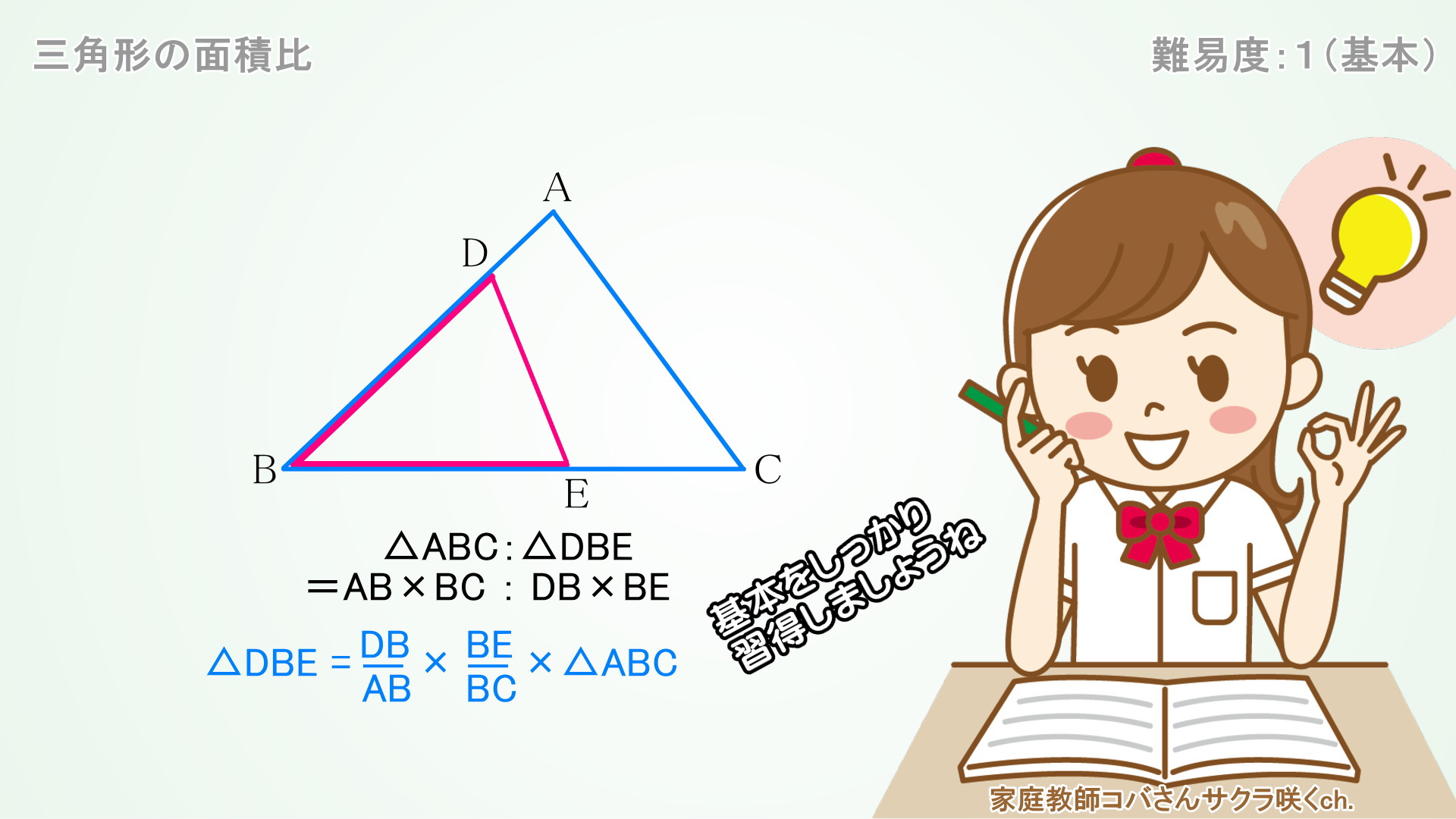
角を共有する三角形の面積比

△ABC:△DBE = AB×BC:DB×BE
これが△ABCと△DBEの面積比になります。
△ABCを基準にすると

なぜこのような比になるのかをYouTubeにアップしていますので是非そちらをご覧ください。
三角形の面積比 練習問題
(1) △ABDは△ABCの面積の何倍か
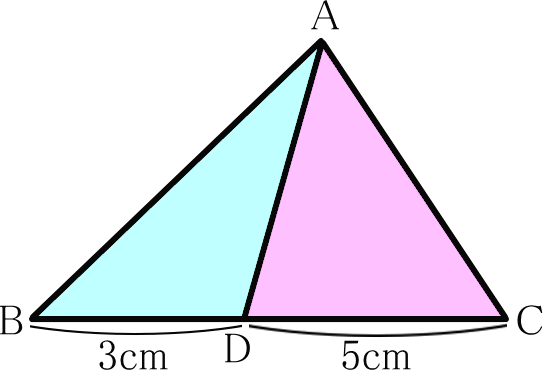
答え 3/8倍
(2) △DBEは△ABCの面積の何倍か
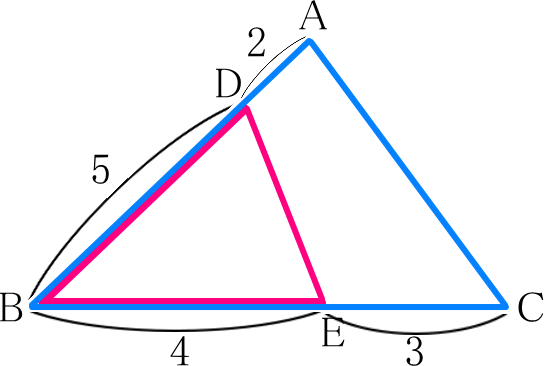
答え 20/49倍
練習問題の解説をYouTubeにアップしていますので是非そちらをご覧ください。
三角形の面積比 解説動画

















コメント