高校受験に役立つテクニック 三角錐の体積

2023年度 東京都 数学 第五問 入試問題過去問 をもとに高校受験に使える技を２件紹介します。

正四面体の体積を求める方法

三角錐にも応用できる時がありますので是非実践に役立ててください。

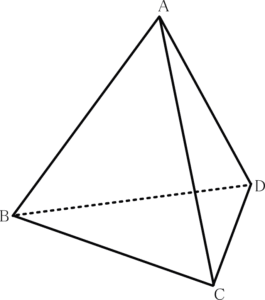
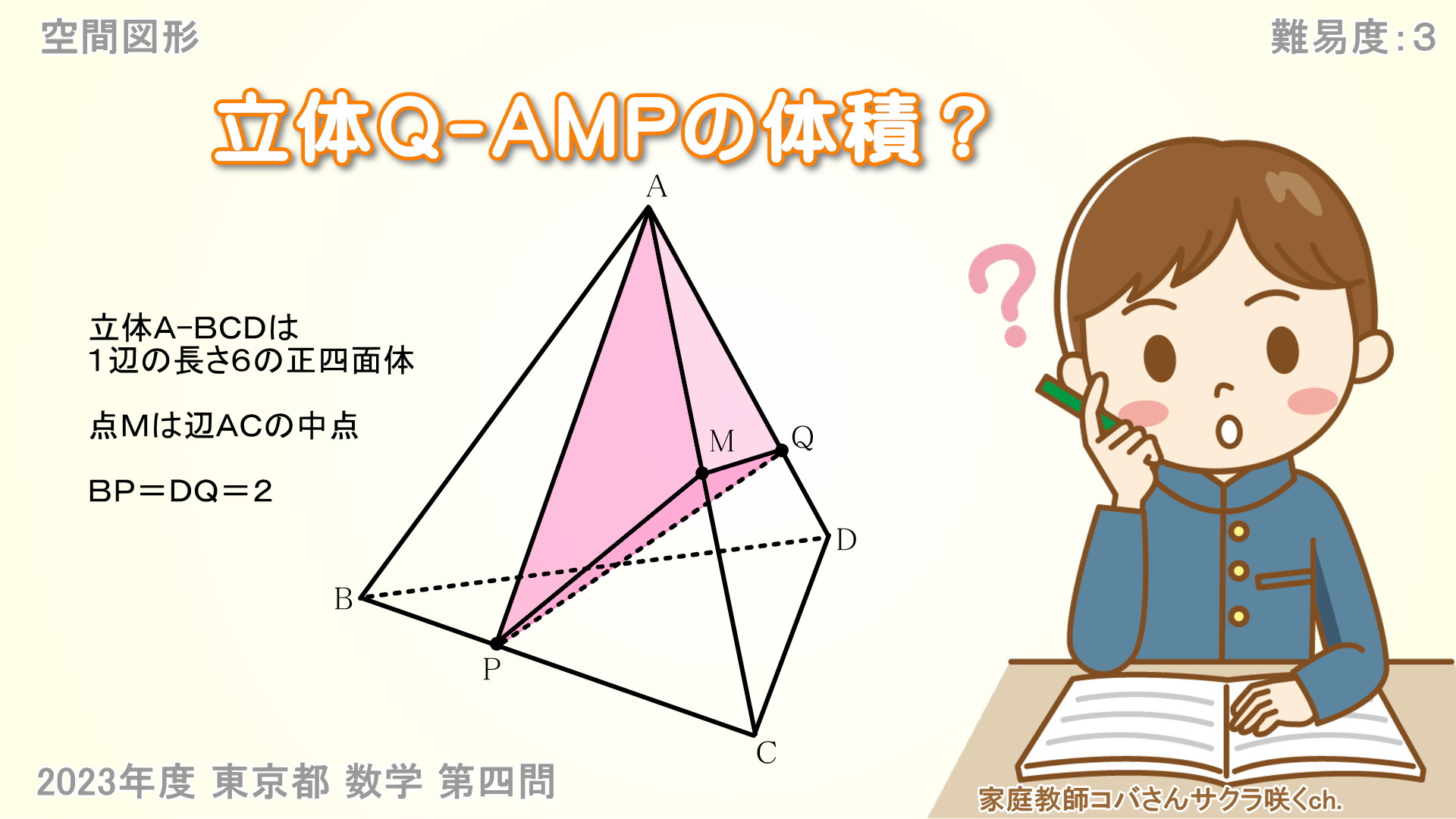
このような一辺が６cmの正四面体（三角すい含む）の体積を求める際に、皆さんはどう解くか？

私も含めて角錐の体積なのだから底面積と高さを求めて解くと思います。
計算すれば底面積も高さもどちらも導くことができます。

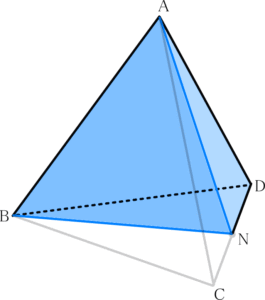
では上図のように正四面体を切断してはどうでしょう？（Nは線分CDの中点）

（さすがに面ABNの面積もあっという間に解くという方法はありません）

このテクニックを知っていると楽に問題を解くことができる、そんな問題が公立高校・私立高校の入試に数多く出題されています。

立体の体積

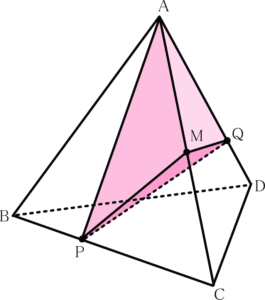
角錐、角柱は底面積と高さからなりますので底面の面積比と高さの比が分かれば大本（おおもと）の体積から求めたい立体の体積を求めることができます。

高校受験に役立つテクニック 三角形の面積比

三角形の面積比を求める基本的な考えを3つ紹介します。入学試験にも三角形の面積を求める問題は数多く出題されています。その面積を求める際に単純に公式通りに底辺と高さを用いる方法もありますが、ベースとなる三角形の面積の何倍になっているのか、面積...

zoom-teacher.com

2023.03.19

以前紹介した三角形の面積比の考え方を平面図形だけでなく空間図形にも応用したもです。
こちらのテクニックを駆使する問題も公立高校・私立高校の入試に数多く出題されていますので是非頭に入れておいてくださいね。

高校受験に役立つテクニック 動画

今回紹介したテクニックを駆使して問題を解いてみてくださいね。