動点４つ 三角形と四角形の面積

2021年度 栃木県 公立高校の入試問題 数学 第５問
動点が４つも出てきて、しかも時間差で動き出す。一見難しそうな問題ですが、グラフを書いて交点を求めれば簡単に解ける問題です。

三角形と四角形の面積が等しくなる点を見つける

問題
図１のようなＡＢ＝１０cm、ＡＤ＝３cmの長方形ＡＢＣＤがある。
点ＰはＡから点ＱはＤから同時に動き出し、ともに毎秒１cmの速さで点Ｐは辺ＡＢ上を点Ｑは辺ＤＣ上を繰り返し往復する。
２点Ｐ、Ｑが動き出してからｘ秒後の△ＡＰＱの面積をｙ㎠とする。
ただし、点ＰがＡにあるときｙ＝Ｏとする。このとき、の(1),(2)，(3)の問いに答えなさい。

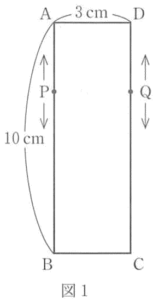
(1) ２点Ｐ、Ｑが動き出してから６秒後の△ＡＰＱの面積を求めなさい。
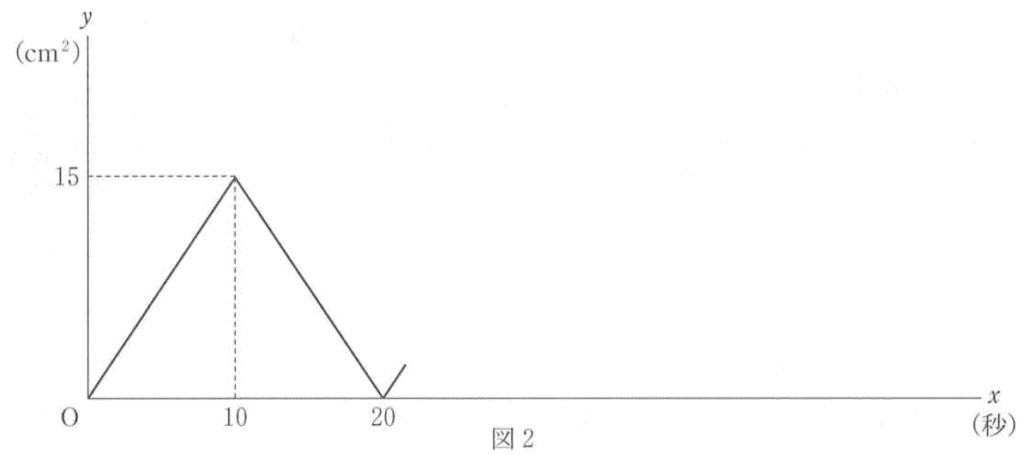
(2) 図２はｘとｙの関係を表したグラフの一部である。２点Ｐ、Ｑが勤き出して１０秒後から
２０秒後までのｘとｙの関係を式で表しなさい。ただし、途中の計算も書くこと。

(3) 点ＲはＡに点ＳはＤにあり、それぞれ静止している。２点Ｐ、Ｑが動き出してから１０秒後に２点Ｒ、Ｓは動き出し，ともに毎秒０.５cmの速さで点Ｒは辺ＡＢ上を点Ｓは辺ＤＣ上を２点Ｐ、Ｑと同様に繰り返し往復する。
　このとき２点Ｐ、Ｑが動き出してからｔ秒後に△ＡＰＱの面積と四角形ＢＣＳＲの面積が等しくなった。
このようなｔの値のうち、小さい方から３番目の値を求めなさい。

解答・解説動画 今回は周期を利用して解く

解き方はいろいろありますが、今回は周期を利用して解こうと思います。

面積が３回目に等しくなる時間を求める問題です。今回は５回目や１０回目、何回目がきても容易に解けるように周期に着目して解いてみました。

出典：栃木県 2021年度 公立高校入試問題 数学 第五問